Una Pared en el Universo

Por Andrei Vazhnov

Hace un par de meses, en una reunión de Instituto Baikal sobre las obras de Platón, estabamos haciendo una ronda de lo que nos llamó antención de la lectura acordada cuando alguién respondió, «Sabes cual es mi opinion sobre esto? No me importa lo que yo opino.» El contexto del comentario era no querer sesgar su evalución de Platón con opiniones premaduras, pero aunque la respuesta tenia cierta logica, la habitación se llenó de risa y el dicho imediatamente se volvió un código interno.

Una de las cosas más fuertes de estas reuniones sobre la filosofia antigua es encontrar en ella los ecos de las ideas modernas — las semillas de las ideas de Bergson, Kant, Freud y muchos otros se ven de forma muy directa en los dialogos de Platón y pensando en el porqué nos resultó tan gracioso este dicho, me acordé de uno de los filosofos aun más antiguos, Epimenides de Knossos que vivió alrededor de 600 a.C.

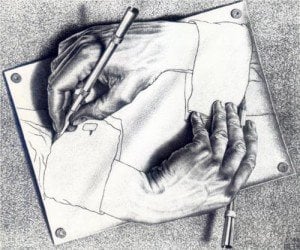
Creo que el core de la gracia de este dicho e ideas parecidas es que si analizamos la oración «No me importa lo que yo opino,» tenemos una situación absurda — si esta en realidadad es mi opinion, supuestamente también incluiria a si misma, lo cual nos llevaría a la conclusion que no me importa esta opinion tampoco, lo cual es una contradicción. Esto es la esencia de la paradoja de Epimenides (que es tan famosa que está incluida en la Biblia, Tito 1:12) — en ésta paradoja, Epimenides, quíén era un habitante de la isla Creta, dice «Todos los Cretenses son mentirosos» (All Cretans are liars). Se ve que esta es una oración imposible — si es verdadera, implica que es falsa y si es falsa, implica que es verdadera. De cierta manera, la oración curiosamente oscilla entre verdad y falsedad y es la idea clave de uno de los resultados más profundos jamas producido por la mente humana — la Teorema de Godel, la cual dice que no importa como construimos nuestro conocimiento logico, siempre habrá verdades escondidas dentro de nuestros sistemas de pensamiento que no podemos alcanzar con nuestro razonamiento. Esto es el tema central del libro Godel, Escher, Bach de Douglas Hofstader y un motif recurrente en la arte de M.C. Escher: por ejemplo, en el cuadro arriba las manos dibujan a si mismas. Esto también es la raiz de de la crisis más importante en la historia de la logica cuya resolución y concecuencias desafian la manera de que normalmente vemos al mundo.

En el comienzo del siglo XX, la matematica enfrentó una serie de problemas que está conocida como la crisis fundacional: paradojas, contradicciones y inconsistencias se iban acumulando rapidamente y segían sin resolución. Un ejemplo de esto es la paradoja de Bertrand Russell que él illustraba así, “En una ciudad todos los hombres se afeitan — algunos se afeitan a si mismos y otros van a un barbero. La definición del barbero, entonces, es la persona que afeita a todos los hombres que no se afeitan a si mismos. Y quién afeita al barbero?” Se ve que si el barbero se afeita a si mismo, no deberia hacerlo por las reglas de la ciudad y si no lo hace sí deberia hacerlo. Las versiones formalmente expresadas de este tipo de paradojas producían contradicciones graves en el razonamiento lógico.

Los matematicos liderados por David Hilbert estaban buscando establecer todo el cuerpo de razonamiento logico de una manera rigorosa sobre una foundación de axiomas. La idea de Hilbert era que si arrancamos con los axiomas cuidadosamente elegidos y aplicamos la logica de una manera objetiva y metodica, podemos construir la matematica libre de contradicción. Bertrand Russell, que después se volvió filosofo, en aquel entonces era uno de los matematicos más conocidos de la epoca y dedicó más de 10 años de su vida a seguir el programa de Hilbert y tratar desarollar la matematica desde principio en su obra Principia Matematica que escribió con Alfred North Whitehead.

El descubrimiento de Godel no solamente puso un fin a estos esfuerzos sino declaró que cualquier esfuerzo de este tipo siempre va a afracasar. Su teorema (en realidad hay dos relacionadas) dice que no importa que axiomas elijas, siempre va a haber proposiciones verdaderas que no se puede comprobar a partir de las axiomas elegidas. O, si tu sistema puede comprobar cualquier proposición, inevitablemente va a contener contradicciones. El impacto fue muy fuerte y reaccionando a la teorema, Russell dijo, «Yo reconocí, por supuesto, que el trabajo de Godel tenía importancia fundamental, pero también me resultó confuso… Se aplicaría esto a la arithmética de un alumno de primaria? Deberiamos pensar que 2+2=4.001? Obviamente esto no es el proposito.»

Es un resultado bastante deprimente especialmente para Russell y todo el programa de Hilbert porque la teorema de Godel impone un limite absoluto para nuestra logica. Implica que nunca habrá Theory of Everything que arranca con principios claros y firmes y de los cuales todo el conocimiento puede ser derivado de forma puramente logica. Godel logró hacer todo esto efictivamente con un tipo de paradoja de Epimenides muy sofisticado. Consideren la oración «Esta oración es falsa.» Al igual que la paradoja de Epimenides es una oración que oscilla entre falsedad y verdad y Godel usó algo parecido. En su teorema, en vez de usar «Esta oración es falsa,» él usó lo siguiente: «Esta proposición no es comprobable» (This statement is unprovable). La genialidad de la teorema es que él logró expresar la oración en terminos de numeros a traves de lo que hoy en día se llama «Godel Numbering.» Y al igual que con la paradoja de Epimenides, la situación es una contradiccion circular que «si tu logica puede comprobar esta oración, se niega a si misma y si no puede hacerlo es incompleta».

Hay mucho disacuerdo acerca de las implicancias filosoficas de Teorema de Godel. Por ejemplo, el matematico/fisico Roger Penrose dice que la teorema demuestra que las verdades vienen de de afuera de la logica humana y afirma la posicion filosofica de «Mathematical Platonism» — o sea que las verdades existen en el mundo ideal (tal como lo imaginaba Platón) y que estas verdades nos llegan a nosotros a través de procesos que en sí no son logicos. Por ejemplo, en su libro «Emperor’s New Mind» Penrose dice «Hay algo absoluto y divino acerca de la verdad matematica. La verdad real de la matematica va más allá de las construcciones humanas» (There is something absolute and God-given about mathematical truth. Real Mathematial truth goes beyond man-made constructions.) El mismo Godel también se consideraba un «Platonist.» Ludwig Wittgenstein, por otro lado, no estaba de acuerdo con este tipo de conclusiones y hay debate hasta hoy en día si él y Russell (que era mentor de Wittgenstein) interpretaron correctamente el resultado de Godel.

Por más que el polemica acerca de implicancias sigue, los resultados de Godel están reconocidos como hitos historicos en el desarollo de la logica y después hubo various otros descubrimientos que fortaleceron la idea de Godel. El matematico Greg Chaitin hizo una extensión de las ideas de Godel realmente chocante. Allen Knutson, Profesor de Matematica de Cornell University dice acerca de Teorema de Chaitin, “Es una teorema increiblemente pertubador. Es como ir al borde del universo y econtrar una pared.” Los detalles de la Teorema de Chatin son dificiles de resumir, pero las implicancias son que las verdades incalcanzables predichos por la Teorema de Godel no son «raras» o «exoticas» como puede parecer a partir de su construcion que describí arriba, sino al contrario — son totalemente comunes. Que tan comunes? Tan comunes que por cada oración que podemos comprobar hay infinitas oraciones posiblemente verdaderas que nunca podemos llegar a comprobar aun en principio. Es como si estuviesemos en una pequeña isla perdida dentro de un mar infinito — todo lo que podemos saber está en esta isla y afuera solo misterio inalcanzable. Realmente una versión moderna (y como dice Allen Knutson bastante pertubadora) del dicho más famoso de Socrates — «Solo sé que no sé nada.»

El astronomo Carl Sagan usaba el termino Los Grandes Descensos (The Great Demotions) para describir la historia humana: primero supimos que la tierra no era en el centro, depués aprendimos que Sol no lo era tampoco; y ahora sabemos que estamos perdidos en el lugar muy promedio entre un sinfin de las galaxias, cada una con centenas de billiones de Soles. El Teorema de Godel y sus extensiones son para mi tal vez el Gran Descenso más fuerte de todos ya que las limitaciones de logica rigen no solo en nuestro rincon ontologico sino también en todos los universos posibles (si ellos existen o han existido).

Sin embargo, como suele pasar, el limite que impuso Godel, a la vez fue la inspiración que impulsó los descubrimientos aun más impactantes. Cuando Alan Turing empezó a escribir su tesis doctoral, su proposito era testear el razonamiento de Godel inventando, como experimento pensando, una machina que pueda automaticamente decidir si una proposición era verdadera o falsa a base de axiomas y reglas de logica. Al final Turing comprobó que Godel tenía razon y que no había manera de esquivar el limite pero dentro de unos años este paper de Turing nos llevó al invento de la computadora digital que hoy en dia determina tantos aspectos de nuestra vida.

Pensando en como los limites a veces empujan creatividad y abren otras puertas, me acordé de la pregunta que hizo Facu en el comienzo de una de las reuniones de Platón. Qué tiene que ver uno con otro los conceptos como «amor por tu pueblo,» «amor romantico,» o «amor por sabiduria?» Por qué usamos la misma palabra para expresar conceptos tan distintos? La respuesta de Platón, explicada a Socrates a través de la protagonista Diotima es que los tres conceptos del amor tienen en común la transcendencia de la muerte — a traves de la sociedad que vive después de vos, a traves tus hijos o tus ideas. El limite siempre nos empuja a trasender.

Y en cuanto a la pared en el universo, tal vez es una bendición. Implica que nunca llegaremos a un punto donde hemos explicado todo con un modelo universal, que la aventura nunca terminará, que aun en el ambito más puro y abstracto siempre habrá contradicciones y misterios por más que crezca nuestro conocimiento. Y en el universo habrá mucho más.

---

Referencias

1. Godel’s Proof by Ernest Nagel y James Newman https://www.amazon.com/G%C3%B6dels-Proof-Ernest-Nagel/dp/0814758371

2. Emperor’s New Mind by Roger Penrose https://www.amazon.com/Emperors-New-Mind-Concerning-Computers/dp/0192861980

3. La Crisis Foundacional en la matematica: https://en.wikipedia.org/wiki/Foundations_of_mathematics#Foundational_crisis

4. Godel’s Theorem and Information: https://www.cs.auckland.ac.nz/~chaitin/georgia.html

Destacaría también que las implicancias filosoficas del Teorema de Chaitin son, al igual que las de Teoerma de Godel, bastante polemicas. Chaitin dice que las implicancias son que las verdades matematicas son contingentes y aleatorias y que la matematica tiene que volverse más parecida a otras ciencias naturales (o sea experimentar más con axiomas). Por lo general, los matematicos y los logicians (e.g. Torkel Franzen) no están de acuerdo con interpretación tan extrema.

5. La paradoja de Russell se trata de un conjunto de todos los conjuntos que no son miembros de sí mismos:
https://en.wikipedia.org/wiki/Russell%27s_paradox

6. Aparte de Turing, Alonzo Church y Emil Post descubrieron las ideas fundacionales de computación de forma independiente.